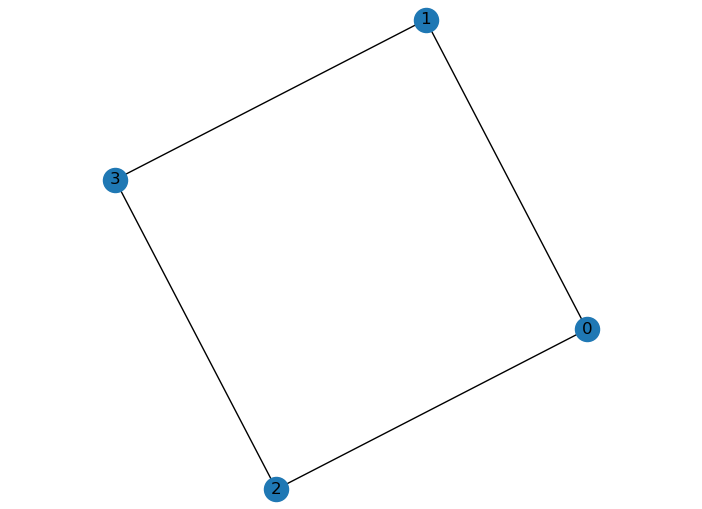
import matplotlib.pyplot as plt import networkx as nx import numpy as np adj = [ [0, 1, 1, 0], [1, 0, 0, 1], [1, 0, 0, 1], [0, 1, 1, 0]] print (adj) G = nx.from_numpy_matrix(np.array(adj)) nx.draw(G, with_labels=True) plt.axis('equal') plt.show()
[[0, 1, 1, 0], [1, 0, 0, 1], [1, 0, 0, 1], [0, 1, 1, 0]]
[PNG image (24.8 KB)]
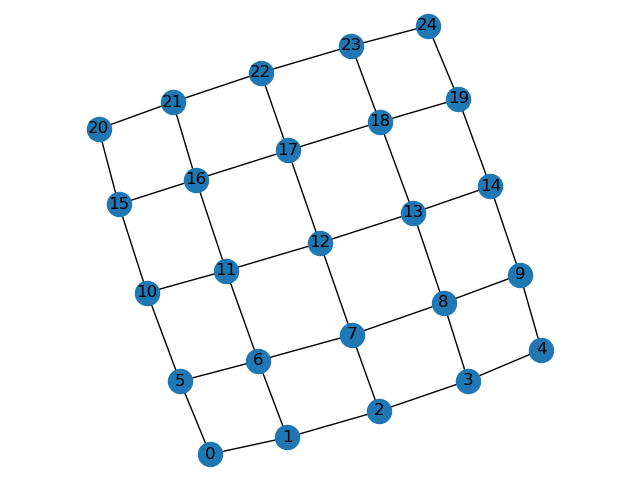
# 5 X 5 adj = np.zeros((25,25)) for i in range(0, 25): u = i - 5 d = i + 5 l = i - 1 r = i + 1 if 0 < u: adj[i][u] = 1 if d < 25: adj[i][d] = 1 if 0 <= l and (l % 5) != 4: adj[i][l] = 1 if r < 25 and (r % 5) != 0: adj[i][r] = 1 print (adj) G = nx.from_numpy_matrix(np.array(adj)) nx.draw(G, with_labels=True) plt.axis('equal') plt.show()
[[0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 1. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 1.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 1. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 1.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0.]]
[PNG image (51.66 KB)]
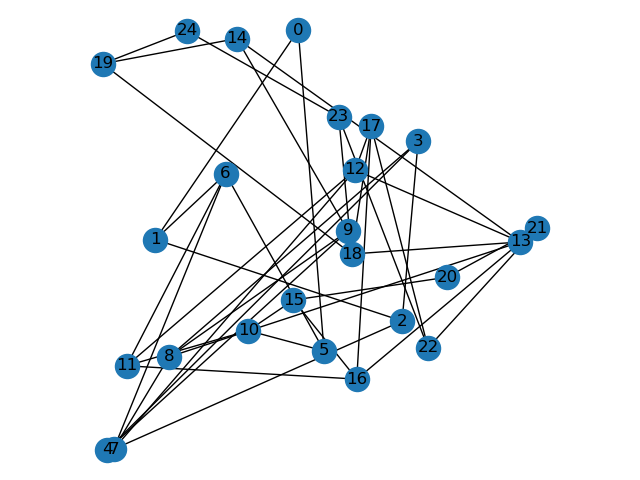
nx.draw_random(G, with_labels=True)
[PNG image (89.05 KB)]
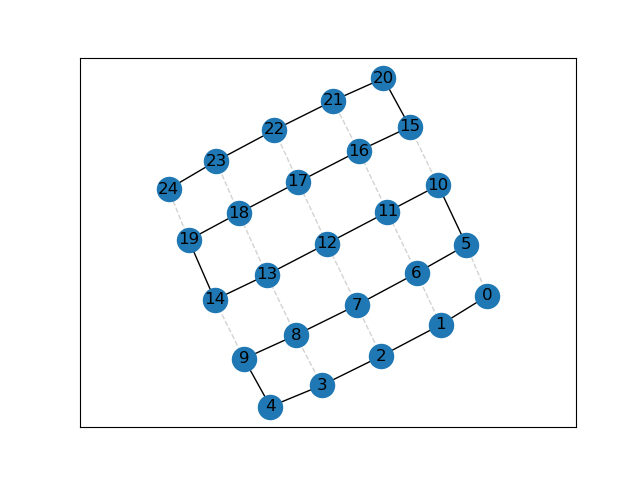
# DFS visualization adj = np.zeros((25,25)) adjTrail = np.zeros((25,25)) visited = np.zeros(25) def dfs(v): global adjTrail global visited visited[v] = 1 for i in range(0, 25): if adj[v][i] and not visited[i]: adjTrail[v][i] = 1 adjTrail[i][v] = 1 dfs(i) for i in range(0, 25): u = i - 5 d = i + 5 l = i - 1 r = i + 1 if 0 < u: adj[i][u] = 1 if d < 25: adj[i][d] = 1 if 0 <= l and (l % 5) != 4: adj[i][l] = 1 if r < 25 and (r % 5) != 0: adj[i][l] = 1 dfs(0) G = nx.from_numpy_matrix(np.array(adj)) pos = nx.spring_layout(G) trail_edges = [(u, v) for (u, v, d) in G.edges(data=True) if adjTrail[u][v] == 1] null_edges = [(u, v) for (u, v, d) in G.edges(data=True) if adjTrail[u][v] == 0] # nodes nx.draw_networkx_nodes(G, pos) # edges nx.draw_networkx_edges(G, pos, edgelist=trail_edges) nx.draw_networkx_edges(G, pos, edgelist=null_edges, edge_color="lightgrey", style="dashed") # labels nx.draw_networkx_labels(G, pos, font_family="sans-serif") plt.axis('equal') plt.show()
0->1->2->3->4->9->8->7->6->5->10->11->12->13->14->19->18->17->16->15->20->21->22->23->24
[PNG image (40.1 KB)]
